Introduction¶
This homework includes the calculation of the different properties of silicon and diamond. Silicon is a brittle crystalline solid in the carbon family (Wikipedia), is a tetravalent metalloid and semiconductor material. In exercise 1 we were assigned to compute the electronic properties of silicon. We first compute the band structure and density of states (DOS) of silicon using the bands calculation methods in DFT, where each orbital of the bands was specified considering their projected DOS. The bandgap is hence obtained from the calculation. To note, the specific $\tt K\_POINT$ path in the Brillouin zone is obtained from Dr. Das's web, to fit the refrence figure. The band gap for Si is then obtained and discussed in comparison with the literature. The effect of the pseudopotentials is specifically discussed as it seems to play a significant role in the final value of the bandgap. The effect of doped Au in Si is then discussed. In exercise 2 the elastic constants of Si and diamond are calculated by applying different types of deformation to the unit cell. The second-order functions are fitted from the DFT computation results using the curve fitting tool in MATLAB. The calculated (fitted) moduli are then compared with literature values from both experiments and computations. I then use bash filed containing for loops to automate the computation processes.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParamsDefault
from datascience import Table
import scipy
%matplotlib inline
Exercise 1: Calculation of the density of states and electronic band structure¶
Exercise 1A¶
Calculate the band structure and density of states for Si using the procedure described above. Prepare plots of the total density of states, and the density of states for each kind of orbital (s, p, d). Assign peaks in the total density of states to atoms/orbitals using information from the atom- and orbital-resolved densities of states. Prepare your plots such that the highest occupied energy level is set to zero energy. What is the chemical character of the valence and conduction bands in Si? Compare your calculated band structure with results from other DFT calculations in the literature. Hint: it may be easier to first locate the relevant papers in the literature and then prepare your band structure plot using the same path through the Brilloiun zone. Hence, you may need to change the information in the K POINTS block in the ’bands’ part of the calculation.
Optimal partameters¶
To begin with, we first test the wave energy cutoff and k point considering the convergence of energy following the procedure of HW1. Similar to HW1, I also obtain the .out files from ESPRESSO using wget from online, then extract the needed values using awk command. The energy cutoff is changed from 20 to 110 Ry and the k point is changed from 1 to 11. Then the optimized lattice constant is calculated using bfgs in ESPRESSO. Taking the same criteria from HW1 as using 5meV for total energy difference, the converged energy cutoff is considered as 30 Ry, and converged k points is 8. The optimized lattice constant is 10.1941 bohr.
# !wget https://hanfengzhai.net/data/MSE5720/Si.20.out https://hanfengzhai.net/data/MSE5720/Si.30.out https://hanfengzhai.net/data/MSE5720/Si.40.out https://hanfengzhai.net/data/MSE5720/Si.50.out https://hanfengzhai.net/data/MSE5720/Si.60.out https://hanfengzhai.net/data/MSE5720/Si.70.out https://hanfengzhai.net/data/MSE5720/Si.80.out https://hanfengzhai.net/data/MSE5720/Si.90.out https://hanfengzhai.net/data/MSE5720/Si.100.out https://hanfengzhai.net/data/MSE5720/Si.110.out
!awk '/!/' Si.20.out Si.30.out Si.40.out Si.50.out Si.60.out Si.70.out Si.80.out Si.90.out Si.100.out Si.110.out
cutoff_1a = np.array([20,30,40,50,60,70,80,90,100,110])
si_energy_cutoff = np.array([-19.21234082,-19.21264567,-19.21273687,-19.21275137,-19.21277846,-19.21278346,-19.21279050,-19.21279347,-19.21279573,-19.21279824])
energy_1a = si_energy_cutoff
energy_difference_cutoff = np.abs(np.array([energy_1a[1]-energy_1a[0],energy_1a[2]-energy_1a[1],energy_1a[3]-energy_1a[2],energy_1a[4]-energy_1a[3],energy_1a[5]-energy_1a[4],energy_1a[6]-energy_1a[5],energy_1a[7]-energy_1a[6],energy_1a[8]-energy_1a[7],energy_1a[9]-energy_1a[8]]))
fig, axs = plt.subplots(1, 2, figsize = (15, 5))
axs[0].plot(cutoff_1a[1:10],np.abs(energy_difference_cutoff), '-.')
axs[0].plot(cutoff_1a[1:10],np.abs(energy_difference_cutoff), 'ro')
axs[0].plot([30, 110], [0.00036749405469679, 0.00036749405469679], '-')
axs[0].text(50, 0.00025, '$\delta_{Energy} = 5$ [meV]')
axs[0].set_xlabel('Planewave cutoff [Ry]')
axs[0].set_ylabel('|$\mathcal{E}_{Energy}$| [Ry]')
axs[0].set_yscale('log')
axs[1].plot(cutoff_1a, si_energy_cutoff, '-.')
axs[1].plot(cutoff_1a, si_energy_cutoff, 'ro')
axs[1].set_xlabel('Planewave cutoff [Ry]')
axs[1].set_ylabel('Energy [Ry]')
It can be observed from the left sub figure that the energy difference converged at 30 Ry.
# !wget https://hanfengzhai.net/data/MSE5720/Si.k.1.out https://hanfengzhai.net/data/MSE5720/Si.k.2.out https://hanfengzhai.net/data/MSE5720/Si.k.3.out https://hanfengzhai.net/data/MSE5720/Si.k.4.out https://hanfengzhai.net/data/MSE5720/Si.k.5.out https://hanfengzhai.net/data/MSE5720/Si.k.6.out https://hanfengzhai.net/data/MSE5720/Si.k.7.out https://hanfengzhai.net/data/MSE5720/Si.k.8.out https://hanfengzhai.net/data/MSE5720/Si.k.9.out https://hanfengzhai.net/data/MSE5720/Si.k.10.out https://hanfengzhai.net/data/MSE5720/Si.k.11.out
!awk '/!/' Si.k.1.out Si.k.2.out Si.k.3.out Si.k.4.out Si.k.5.out Si.k.6.out Si.k.7.out Si.k.8.out Si.k.9.out Si.k.10.out Si.k.11.out
kpoint_1a = np.array([1,2,3,4,5,6,7,8,9,10,11])
energy_1a_k = np.array([-17.97654358,-19.06512494,-19.21277846,-19.24591070,-19.25554605,-19.25874215,-19.25990033,-19.26034856,-19.26053082,-19.26060791,-19.26064150])
energy_difference_k = np.abs(np.array([energy_1a_k[1]-energy_1a_k[0],energy_1a_k[2]-energy_1a_k[1],energy_1a_k[3]-energy_1a_k[2],energy_1a_k[4]-energy_1a_k[3],energy_1a_k[5]-energy_1a_k[4],energy_1a_k[6]-energy_1a_k[5],energy_1a_k[7]-energy_1a_k[6],energy_1a_k[8]-energy_1a_k[7],energy_1a_k[9]-energy_1a_k[8],energy_1a_k[10]-energy_1a_k[9]]))
fig, axs = plt.subplots(1, 2, figsize = (15, 5))
axs[0].plot(kpoint_1a[1:11],np.abs(energy_difference_k), '-.')
axs[0].plot(kpoint_1a[1:11],np.abs(energy_difference_k), 'ro')
axs[0].plot([2,11], [0.00036749405469679, 0.00036749405469679], '-')
axs[0].text(2, 0.0005, '$\delta_{Energy} = 5$ [meV]')
axs[0].set_xlabel('Planewave cutoff [Ry]')
axs[0].set_ylabel('|$\mathcal{E}_{Energy}$| [Ry]')
axs[0].set_yscale('log')
axs[1].plot(kpoint_1a, energy_1a_k, '-.')
axs[1].plot(kpoint_1a, energy_1a_k, 'ro')
axs[1].set_xlabel('Planewave cutoff [Ry]')
axs[1].set_ylabel('Energy [Ry]')
From the left sub figure it can be deduced that the converged k point is 9.
Changing the calculation methods from scf to vc-relax, and following the same procedure in HW1, the optimized lattice constant is obtained from bfgs.
- The optimized lattice constant is 10.1941 Ry.
According to NIST, the lattice constant for silicon is $5.431 020 511 \times 10^{-10}\rm m$, which is $10.2646\ \rm bohr$. Hence, taking the NIST result as a reference, our converged value has a relative error of $0.6868\%$.
Band structure¶
Now we compute the band sturcture of silicon. To better illustrate how the k point in integrated in the microstructure, the following figure is included: the band structure is calculated by integrating the energy on the path: $L → \Gamma → X → U → Γ$, as can be illustrated in the following figure (Hakl, 2012).

Followed, the band structures are computed from ESPRESSO. Following the procedure given, I change the command to ibrav=0 and modify the $\tt K\_POINT$ based on the list from Dr. Das:
K_POINTS {crystal_b}
5
0.0000 0.5000 0.0000 20 !L
0.0000 0.0000 0.0000 30 !G
-0.500 0.0000 -0.500 10 !X
-0.375 0.2500 -0.375 30 !U
0.0000 0.0000 0.0000 20 !G
If compared with the band structure from Niquet et al. (2009), as can be observed from $Γ → X → W → L → Γ$ in their figure (full horizontal axis in my figure), the general band structures are captured with a mild feature difference from the points in the middle regime ($X → U$ in my approach and $X → W → L$ in their approach).

![]()
![]()
- The chemical character of the band structure is the band possesses an indirect gap.
Regarding to this "mild difference" from my calculation and their's, I proposed the following discussion:
The work by Niquet et al. integrate the k points differently, causing the mild difference in the area around $W$ and $L$ with $U$. Variation of the k path variate the final band structure. Specifically, the robustness of orbital interactions will affect the density of the final band structure (Lamontagne, 2018).
# !wget https://hanfengzhai.net/data/MSE5720/Si_dos.txt https://hanfengzhai.net/data/MSE5720/Si_s_pdos.txt https://hanfengzhai.net/data/MSE5720/Si_p_pdos.txt
def data_loader(fname):
fid = open(fname, "r")
data = fid.readlines()
fid.close()
energy = []
pdos = []
for row in range(len(data)):
data_row = data[row]
if (data_row[0][0] != '#'):
data_row = data_row[:-1].split(' ')
energy.append(float(data_row[1]))
pdos.append(float(data_row[3]))
energy = np.asarray(energy)
pdos = np.asarray(pdos)
return energy, pdos
energy, pdos_s = data_loader('Si_s_pdos.txt')
_, pdos_p = data_loader('Si_p_pdos.txt')
_, pdos_tot = data_loader('Si_dos.txt')
energy = energy - 6.22
# make plots
plt.figure(figsize = (10, 5))
plt.plot(energy, pdos_s, linewidth=1, color='b', label='s-orbital')
plt.plot(energy, pdos_p, linewidth=1, color='r', label='p-orbital')
plt.plot(energy, pdos_tot, linewidth=1, color='g', label='total')
# plt.yticks([])
plt.xlabel('$E - E_f$ (eV)')
plt.ylabel('DOS')
plt.axvline(x = 0, linewidth=0.5, color='k', linestyle=(0, (8, 10)))
# plt.xlim(-6, 16)
plt.ylim(0, 2)
plt.fill_between(energy, 0, pdos_s, where=(energy < 0), facecolor='b', alpha=0.25)
plt.fill_between(energy, 0, pdos_p, where=(energy < 0), facecolor='r', alpha=0.25)
plt.fill_between(energy, 0, pdos_tot, where=(energy < 0), facecolor='g', alpha=0.25)
plt.text(-0.5, 1.2, 'Fermi energy', rotation=90)
plt.legend(frameon=False)
plt.show()
The above figure shows both the DOS and PDOS of silicon. To verify the DOS, a reference figure is adopted from Argonne National Lab shown as below:

It can be observed that the DFT computed DOS has generally similar trends (with major characteristics captured) compared with the reference figure: there are three main peaks under the occupied region and one big ocsillating bigger peak in the unoccupied region. The occupired region ranges from $∼$15eV to 0 and the unoccupied region ranges from $∼$0.5eV to $∼$10eV.
To verify the accurate calculation of PDOS, a reference figure is obtained from plotly, made by Prof. Vallverdu, shown as below:
![]()
Comparing the ESPRESSO calculated PDOS (blue line stands for s orbital, red line stands for p orbital, and green line stands for total PDOS in my approach) with the above figure, the PDOS basically matches with similar trends: the green line from the above figure with the red line in my figure possess very similar trends, the red line from above also possess similar trends with my blue line.
Exercise 1B¶
What is the band gap for Si? Is Si a direct or indirect gap insulator? How does your gap compare with experiment, and with other DFT calculations in the literature?
There are many ways to obtain the band gap from DFT. Here, I examine two of which to test my results either directly extracted from the energy difference from the .out file, or plot the DOS and compute the length of the "zero value regime".
# !wget https://hanfengzhai.net/data/MSE5720/Si.out
!awk '/highest/' Si.out
band_gap = 6.7077 - 6.2200; print(band_gap)
Hence the band gap obtained from DFT is approximately 0.49eV.
- The second way to compute band gap is through capturing the length of the "zero value regime" in the DOS plot.
To compute the band gap, instead of taking the default value of $Δ E = 0.1\rm eV$, we increase the energy discretization density to $Δ E = 0.01\rm eV$ and the compared figure is shown as below.
![]()
- Using this method, the computed band gap is $6.67 - 6.22 = 0.45 \rm eV$.
Here, due to the Fermi level being in the bandgap (Ref. link) for silicon. We can therefore say silicon is a semiconductor. Compared with the reference data from Singh et al. (2013), the LDA computed band gap of silicon is 0.49eV, where the relative of our value is $8.16\%$, which is an acceptable value. If taking the value of 0.49eV from directly calculating the difference from the .out file shown above, the relative error is $0\%$. However, the actual experimental measured band gap is 1.12eV (Toshiba website). Obviously, the LDA computed bandgap is not so accurate. As proposed by Persson and Mirbt (2006): "if a too strong electron-electron repulsion within LDA, the electron (wavefunction) overlap is too small and thus also the semiconductor band gap becomes too small." This finding perfectly explains our inaccurate computation of silicon band gaps.
Exercise 1C¶
Examine the DOS for bulk Si and Si doped with Au in Figure 2 (from Sholl & Steckel, 2009). Pay particular attention to the DOS at the band gap. Now read Nature Materials 4 676 (2005). How do you think the presence of Au affects the performance of Si in solar cells?
From Fig. 2 (HW), there are two evident peaks occurring at $E \approx 0\rm eV$ and $E \approx 5\rm eV$ (bandgap regime) for Au doped Si compared with pure Si. Just from this figure, we can conclude that the existence of Au changes the DOS of the bandgap region, leading to an obvious density of states "peak" existing in the bandgap region of Au doped silicon which is more similar to conductors rather than semiconductors. From the differences in DOS, we can further conclude that the existence of Au changes the occupancy of the electrons in Si. The major electric conductivity does not variate much. Referring to Buonassisi et al., it is stated that metal-contained semiconductors can still be viewed as accepted material for solar cells since nano defect engineering can reduce the electronic characteristic of the metal impurities. Also, from the mentioned existing metal particles that will change the diffusion length of the carrier we can further conclude that existing Au changes the electronic diffusion and further DOS of the silicon. Hence, combining both the viewpoints we can deduce that the existence of metal nano-defect in Si changes the occupancy of electrons and further the diffusion length, which variates its electronic properties. Specifically, the Au caused "bandgap diminishment" leads to decreased efficiency of Si-based solar cells.
Exercise 2: Calculation of elastic constants¶
Exercise 2A¶
Calculate $C_{11}$, $C_{12}$ and $C_{44}$ for both diamond and Si following the procedure above. Calculate the total energy as a function $U$ for $\eta$ = -0.006, -0.004, -0.002, 0.002, 0.004 and 0.006. Fit the energy change per unit volume ($\Delta U / \Omega$) for each value of $\eta$ to Equations 2, 3 and 4 to obtain the elastic constants (note that the zero distortion point must also be part of your fit: $\Delta U / \Omega=0$, $\eta = 0$).
The isotropic, tetragonal, and trigonal deformations are applied to the silicon unit cell, respectively, using the relax computation method. The total energies are hence obtained using awk command. The data were fitted using the MATLAB $\tt curve \ fitting$ toolbox. The uncertainty range are presented and the fitted values are readjusted from the curve fitting. The calculated elastic constants were compared with literature values.
- Silicon under isotropic deformation:
# !wget https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.497.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.498.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.499.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.500.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.501.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.502.out https://hanfengzhai.net/data/MSE5720/Si_isotro.cell_0.503.out
!awk '/!/' Si_isotro.cell_0.497.out Si_isotro.cell_0.498.out Si_isotro.cell_0.499.out Si_isotro.cell_0.500.out Si_isotro.cell_0.501.out Si_isotro.cell_0.502.out Si_isotro.cell_0.503.out
!awk '/volume/' Si_isotro.cell_0.497.out Si_isotro.cell_0.498.out Si_isotro.cell_0.499.out Si_isotro.cell_0.500.out Si_isotro.cell_0.501.out Si_isotro.cell_0.502.out Si_isotro.cell_0.503.out
- Silicon under tetragonal deformation:
# !wget https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.497.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.498.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.499.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.500.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.501.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.502.out https://hanfengzhai.net/data/MSE5720/Si_tt.cell_0.503.out
!awk '/!/' Si_tetra.cell_0.497.out Si_tetra.cell_0.498.out Si_tetra.cell_0.499.out Si_tetra.cell_0.500.out Si_tetra.cell_0.501.out Si_tetra.cell_0.502.out Si_tetra.cell_0.503.out
!awk '/volume/' Si_tetra.cell_0.497.out Si_tetra.cell_0.498.out Si_tetra.cell_0.499.out Si_tetra.cell_0.500.out Si_tetra.cell_0.501.out Si_tetra.cell_0.502.out Si_tetra.cell_0.503.out
The obtained energy and volume values based on different $\eta$ were then substitute into the Equations. $C_{11}$ and $C_{12}$ were then solved from Equations ($2$) and ($3$). To specify the uncertainty during the curve fitting, the range of the fitting data were also presented below.
from sympy import *
C11 = Symbol('C11')
C12 = Symbol('C12')
eqs = [-19.26023079 - (-19.26022306) - 266.4341*1.5*(C11+2*C12)*4e-6,\
-19.26023079 - (-19.26022306) - 266.4341*3*(C11-C12)*4e-6]
solu_2 = solve(eqs, [C11, C12])
solu_2
vol_Si_iso = np.array([265.1803,266.7842,268.3946,270.0114,271.6347,273.2645,274.9008])
lat_Si = np.array([-0.006,-0.004,-0.002,0,0.002,0.004,0.006])
Ener_Si_iso = np.array([-19.26022905,-19.26022374,-19.26015209,-19.26001820,-19.25982786,-19.25957495,-19.25926397])
vol_Si_tetra = np.array([269.9823,269.9985,270.0082,270.0114,270.0081,269.9984,269.9821])
Ener_Si_tetra = np.array([-19.26007342,-19.26035228,-19.26052123,-19.26057737,-19.26052096,-19.26034777,-19.26005644])
EnerSi_iso_fit = (Ener_Si_iso - (-19.26001820))/270.0114
EnerSi_tetra_fit = (Ener_Si_tetra - (-19.26057737))/264.8419
EnerSi_tetra_fit = np.abs(EnerSi_tetra_fit)
def Si_fit_iso(lat_Si, const1):
return 1.5* (const1)*(lat_Si)**2
popt_iso, pcov_iso = scipy.optimize.curve_fit(Si_fit_iso, lat_Si, EnerSi_iso_fit)
print(popt_iso)
We first trying to solve $C_{11}$ and $C_{12}$ by applying isotropic and tetragonal deformation to the silicon unit cell and fitting the curve:
- For isotropic deformation:
![]()
From the data fitting it is obtained that the fitted $\frac{3}{2}(C_{11} + 2C_{12}) \approx 0.03 \times 14710.5 \rm GPa$; hence: $C_{11} + 2C_{12} = 294.2100 \rm GPa$. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.02907, 0.03]$, where the fitting $R^2$ is 0.9999.
- For tetragonal deformation:
![]()
From the data fitting it is obtained that the fitted $3(C_{11} - C_{12}) \approx 0.02 \times 14710.5 \rm GPa$; hence: $C_{11} - C_{12} = 98.5603 \rm GPa$. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.01948, 0.02001]$, where the fitting $R^2$ is 0.9999.
We can therefore solve for $C_{11}$ and $C_{12}$:
from sympy import *
C11 = Symbol('C11')
C12 = Symbol('C12')
eqs = [C11 + 2*C12 - 294.2100,\
C11 - C12 - 98.5603]
silicon_solu = solve(eqs, [C11, C12])
print(silicon_solu)
It is thence obtained that the elastic constant for silicon are: $C_{11} = 163.78\rm GPa$ and $C_{12} = 65.22\rm GPa$.
Compared with the results from Hall (1967) with $C_{11}$ and $C_{12}$ equals 165.64 and 63.94GPa, respectively, my results have relative errors of $1.12\%$ and $2 \%$, respectively, which can be considered as good accuracy.
# !wget https://hanfengzhai.net/data/MSE5720/Si_tri.cell_1.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_2.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_3.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_4.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_5.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_6.out https://hanfengzhai.net/data/MSE5720/Si_tri.cell_7.out
!awk '/Final/' Si_tri.cell_1.out Si_tri.cell_2.out Si_tri.cell_3.out Si_tri.cell_4.out Si_tri.cell_5.out Si_tri.cell_6.out Si_tri.cell_7.out
The elastic constant $C_{44}$ can then be calculated by applying the trigonal deformation to the silicon unit cell:
![]()
It can be concluded from curve fitting that $\frac{1}{2}C_{44} \approx 0.00259 \times 14710.5\rm GPa$ $→$ $ C_{44} = 76.4946\rm GPa$. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.002304, 0.00259]$, where the fitting $R^2$ is 0.9987.
The k point and energy cutoff for the convergent energy of diamond are then calculated following the same procedure from HW 1.
Diamond_energy_cutoff = np.array([-22.29597645,-23.03782401,-23.05495035,-23.05603958,-23.05667118,-23.05671926,-23.05703253,-23.05730891,-23.05738074,-23.05738699,-23.05747302,-23.05759346])
Diamond_cutoff = np.arange(0,120,10)
Diamond_energy_ecut_diff = np.array([Diamond_energy_cutoff[1]-Diamond_energy_cutoff[0],Diamond_energy_cutoff[2]-Diamond_energy_cutoff[1],\
Diamond_energy_cutoff[3]-Diamond_energy_cutoff[2],Diamond_energy_cutoff[4]-Diamond_energy_cutoff[3],\
Diamond_energy_cutoff[5]-Diamond_energy_cutoff[4],Diamond_energy_cutoff[6]-Diamond_energy_cutoff[5],\
Diamond_energy_cutoff[7]-Diamond_energy_cutoff[6],Diamond_energy_cutoff[8]-Diamond_energy_cutoff[7],\
Diamond_energy_cutoff[9]-Diamond_energy_cutoff[8],Diamond_energy_cutoff[10]-Diamond_energy_cutoff[9],\
Diamond_energy_cutoff[11]-Diamond_energy_cutoff[10]])
fig, axs = plt.subplots(1, 2, figsize = (15, 5))
axs[0].plot(Diamond_cutoff[0:11],np.abs(Diamond_energy_ecut_diff), '-.')
axs[0].plot(Diamond_cutoff[0:11],np.abs(Diamond_energy_ecut_diff), 'ro')
axs[0].plot([0, 100], [0.00036749405469679, 0.00036749405469679], '-')
axs[0].text(50, 0.0005, '$\delta_{Energy} = 5$ [meV]')
axs[0].set_xlabel('Planewave cutoff [Ry]')
axs[0].set_ylabel('|$\mathcal{E}_{Energy}$| [Ry]')
axs[0].set_yscale('log')
axs[1].plot(Diamond_cutoff, Diamond_energy_cutoff, '-.')
axs[1].plot(Diamond_cutoff, Diamond_energy_cutoff, 'ro')
axs[1].set_xlabel('Planewave cutoff [Ry]')
axs[1].set_ylabel('Energy [Ry]')
From the figure it can be concluded that the converged energy cutoff is 40 Ry.
Diamond_energy_kpoint = np.array([-20.86940192,-22.82442708,-23.01464498,-23.04709100,-23.05423188,-23.05601252,-23.05649305,-23.05662877,-23.05666961,-23.05668208,-23.05668542])
Diamond_kpoint = np.arange(0,11,1)
Diamond_energy_ecut_diff = np.array([Diamond_energy_kpoint[1]-Diamond_energy_kpoint[0],Diamond_energy_kpoint[2]-Diamond_energy_kpoint[1],\
Diamond_energy_kpoint[3]-Diamond_energy_kpoint[2],Diamond_energy_kpoint[4]-Diamond_energy_kpoint[3],\
Diamond_energy_kpoint[5]-Diamond_energy_kpoint[4],Diamond_energy_kpoint[6]-Diamond_energy_kpoint[5],\
Diamond_energy_kpoint[7]-Diamond_energy_kpoint[6],Diamond_energy_kpoint[8]-Diamond_energy_kpoint[7],\
Diamond_energy_kpoint[9]-Diamond_energy_kpoint[8],Diamond_energy_kpoint[10]-Diamond_energy_kpoint[9]])
fig, axs = plt.subplots(1, 2, figsize = (15, 5))
axs[0].plot(Diamond_kpoint[0:10],np.abs(Diamond_energy_ecut_diff), '-.')
axs[0].plot(Diamond_kpoint[0:10],np.abs(Diamond_energy_ecut_diff), 'ro')
axs[0].plot([0, 9], [0.00036749405469679, 0.00036749405469679], '-')
axs[0].text(2, 0.0005, '$\delta_{Energy} = 5$ [meV]')
axs[0].set_xlabel('k point')
axs[0].set_ylabel('|$\mathcal{E}_{Energy}$| [Ry]')
axs[0].set_yscale('log')
axs[1].plot(Diamond_kpoint, Diamond_energy_kpoint, '-.')
axs[1].plot(Diamond_kpoint, Diamond_energy_kpoint, 'ro')
axs[1].set_xlabel('k point')
axs[1].set_ylabel('Energy [Ry]')
From the figure it can be concluded that the converged k point is 6.
Now we will calculate the optimized lattice constant of diamond. Taking the optimal k point and energy cutoff, we substitute them and change the calculation to vc-relax. The optimized lattice constant is $6.6740$ bohr.
# !wget https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.497.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.498.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.499.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.500.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.501.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.502.out https://hanfengzhai.net/data/MSE5720/Diamond_iso.0.503.out
# !wget https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.497.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.498.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.499.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.500.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.501.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.502.out https://hanfengzhai.net/data/MSE5720/Diamond_tet.0.503.out
!awk '/Final/' Diamond_iso.0.497.out Diamond_iso.0.498.out Diamond_iso.0.499.out Diamond_iso.0.500.out Diamond_iso.0.501.out Diamond_iso.0.502.out Diamond_iso.0.503.out
!awk '/volume/' Diamond_iso.0.497.out Diamond_iso.0.498.out Diamond_iso.0.499.out Diamond_iso.0.500.out Diamond_iso.0.501.out Diamond_iso.0.502.out Diamond_iso.0.503.out
!awk '/Final/' Diamond_tet.0.497.out Diamond_tet.0.498.out Diamond_tet.0.499.out Diamond_tet.0.500.out Diamond_tet.0.501.out Diamond_tet.0.502.out Diamond_tet.0.503.out
!awk '/volume/' Diamond_tet.0.497.out Diamond_tet.0.498.out Diamond_tet.0.499.out Diamond_tet.0.500.out Diamond_tet.0.501.out Diamond_tet.0.502.out Diamond_tet.0.503.out
Mechanical properties of diamond¶
Diamond under isotropic deformation for computing $C_{11}$ and $C_{12}$.
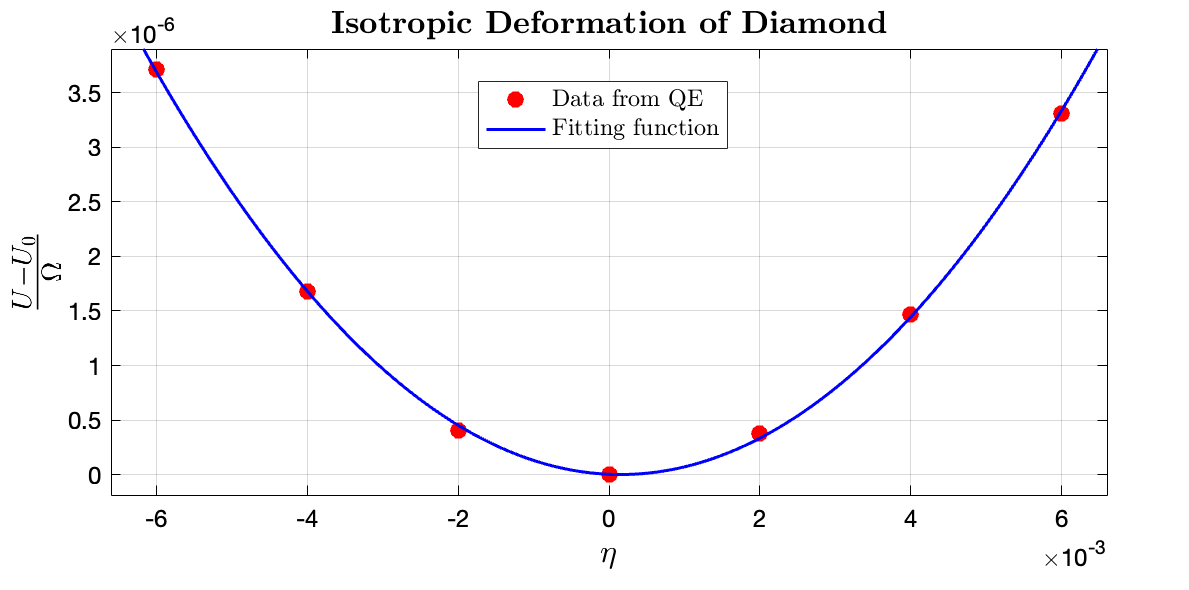
From the MATLAB Curve Fitting Tool, it can be observed that the fitting value for $\frac{3}{2} (C_{11}+2C_{12}) \approx 0.15 \times 14710.5 \rm GPa$, $\longrightarrow (C_{11}+2C_{12}) =1471.1\rm GPa $. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.135, 0.1583]$, where the fitting $R^2$ is 0.9967.
Diamond under tetrahetron deformation
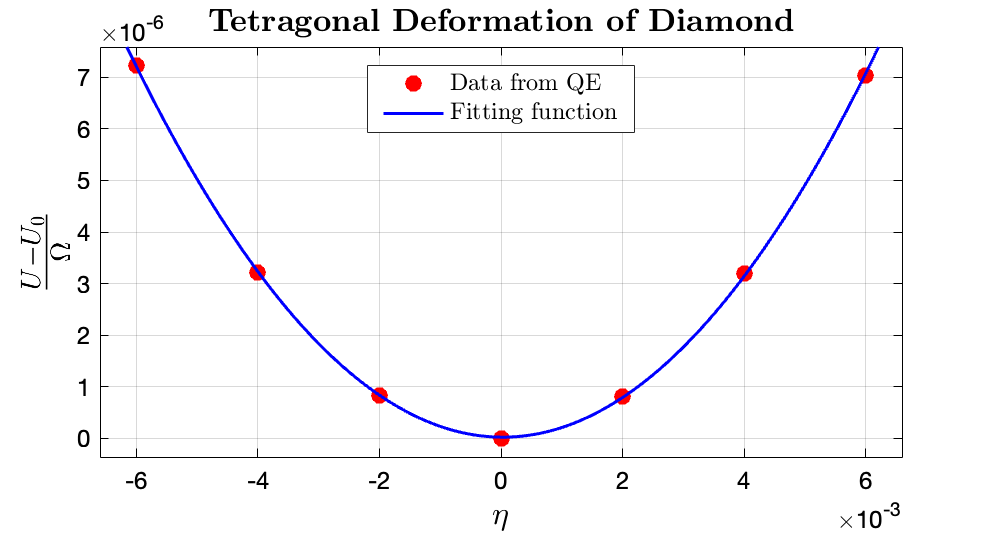
From the MATLAB Curve Fitting Tool, it can be observed that the fitting value for $3 (C_{11}-C_{12}) \approx 0.19 \times 14710.5 \rm GPa$, $\longrightarrow (C_{11}-C_{12}) =931.1746\rm GPa $. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.1949, 0.2003]$, where the fitting $R^2$ is 0.9999.
We can hence solve the equations for $C_{11}$ and $C_{12}$:
from sympy import *
C11 = Symbol('C11')
C12 = Symbol('C12')
eqs = [C11 + 2*C12 - 1471.1,\
C11 - C12 - 931.17]
diamond_solu = solve(eqs, [C11, C12])
print(diamond_solu)
From the data fitting it can be deduced that the computed elastic constants: $C_{11}$ and $C_{12}$ equals 1111.15 and 179.97 GPa, respectively. Compared with the experimental value of $C_{11}, C_{12} = 1078.3, 126.5\rm GPa$, respectively, by Migliori et al. (2008), my computation results have relative errors of $3.05\%$ and $42.27\%$, respectively. It can be observed that the $C_{11}$ has good accuracy whereas $C_{12}$ does not have a good prediction accuracy. However, if compared with also the computation methods proposed by Shao et al. (2012), the prediction of $C_{12}$ by the two different computation methods proposed by the author was 160.2 and 169.1 GPa, where my computation results have relative errors of $12.3\%$ and $6.39\%$, respectively. Although the relative errors are still relatively large, the results can be considered as acceptable. It is hence concluded that the computation for $C_{12}$ tend to exhibits higher errors.
Diamond under trigonal deformation:
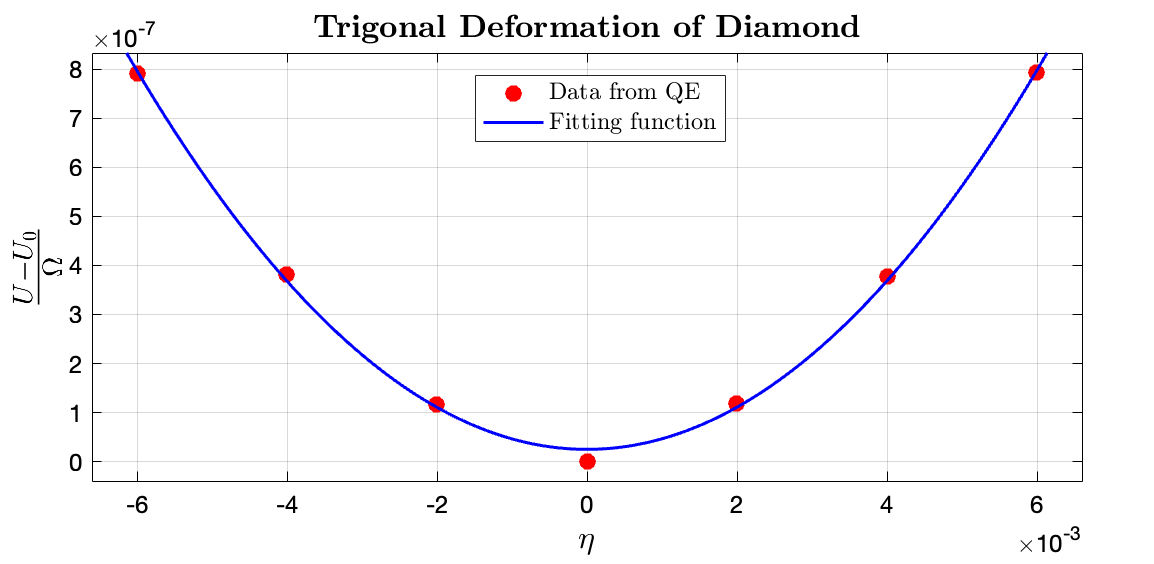
From the data fitting results of MATLAB curve fitting results, it can be deduced that $\frac{1}{2} C_{44} = 0.0202 \times 14710.5 \rm GPa$. The fitting data for $\frac{U - U_0}{\Omega}$ to $\eta$ in $\rm Ry/bohr^3$ range is $\tt [0.02025, 0.02269]$, where the fitting $R^2$ is 0.9975. We can hence solve for $C_{44} = 588.4200\rm GPa$. Compared with the experimental results of 577.5 GPa by Migliori et al. (2008), my result has a relative error of $1.89\%$, which has a decent accuracy.
!awk '/!/' Diamond.0.497.out Diamond.0.498.out Diamond.0.499.out Diamond.0.500.out Diamond.0.501.out Diamond.0.502.out Diamond.0.503.out
!awk '/volume/' Diamond.0.497.out Diamond.0.498.out Diamond.0.499.out Diamond.0.500.out Diamond.0.501.out Diamond.0.502.out Diamond.0.503.out
lat_diamond = lat_Si
Ener_Diamond = np.array([-23.05552571,-23.05567272,-23.05570645,-23.05563344,-23.05545233,-23.05516837,-23.05477257])
plt.plot(lat_diamond,Ener_Diamond)
Exercise 2B¶
How do your results compare with experiment and with other calculations from the literature?
As compared previously, for silicon, the elastic constants are: $C_{11} = 163.78\rm GPa$, $C_{12} = 65.22\rm GPa$, & $ C_{44} = 76.4946\rm GPa$. If taking the experimental data by Hall (1967) as a reference, the relative errors for elastic constants are 1.1229%, 2%, and 3.79%, respectively. If taking the computation results using the LDA pseudopotential by Barhoumi et al. (2021) as a reference, the relative errors for elastic constants are 2.11%, 0.65%, and 1.38%, respectively. For diamond, the computed elastic constants are $C_{11}, C_{12} = 1078.3, 126.5\rm GPa$, and $C_{44} = 588.4200\rm GPa$, respectively. If taking the experimental data from McSkimin and Andreatch (1972) as references, the relative errors are 0.0649%, 2.02%, and 1.8%, respectively. If compared with the computation results using the LDA pseudopotential by Barhoumi et al. (2021), the relative errors are 2.47%, 15.33% and 0.71%, respectively.
Exercise 3¶
In this exercise I wrote different bash files containing different for loops to automate the computation process through going through the targeted values. This allows the script to automatically generate all the in files and run them to generate the out files for postprocessing. There is also a modified .py file for cubic deformation elastic constants computation. The bash files contain both isotropic, tetragonal, and trigonal deformations. To obtain the bash script I wrote, the wget command is still adopted:
!wget https://hanfengzhai.net/data/MSE5720/Si_iso.sh https://hanfengzhai.net/data/MSE5720/Si_tetra.sh https://hanfengzhai.net/data/MSE5720/Si_tri.sh https://hanfengzhai.net/data/MSE5720/diamond_iso.sh https://hanfengzhai.net/data/MSE5720/diamond_tetra.sh https://hanfengzhai.net/data/MSE5720/diamond_tri.sh https://hanfengzhai.net/data/MSE5720/convergence_script.py https://hanfengzhai.net/data/MSE5720/create_scf_file.py https://hanfengzhai.net/data/MSE5720/cub_elastic_const_runjobs.py
Summary¶
In this homework, there are three exercises majorly covering the DFT calculation of electronic and elastic properties of silicon and diamond. In exercise 1, the electronic property, i.e. density of states, projected density of states, band structure, bandgap, and nano-defect influence on the electronic conductance. In exercise 2 we were assigned to compute the elastic constants of diamond and silicon by changing the deformation of the unit cells in isotropic, tetragonal, and trigonal forms. The elastic constants are then obtained by fitting the curve using MATLAB. The resultant values were compared with the literature values and discussed.
There are many difficulties encountered during the process. To elaborate them, I hereby listed with the solution I came up with to solve the problems:
Initially, the bandgap does not fit any reference data from online or reference, thanks to the tutorial of Pranab, I changed my $\tt K\_POINTS$ based on his reference, and the resultant band structure actually looks like the literary figure.
The data fitting from 2 always land in different values and mild change leads to a huge difference. Especially, directly fitting the data using the
script.optimize.curve_fitfunction (link) results in only one value that does not always land in the correct range. Hence, I fit the data using the MATLAB curve fitting tool, where the fitted parameters land in a probabilistic range so that one can pick a value that is more fitted in the correct range based on the experimental value or other computation results.
References¶
[1] Yakovkin and Dowben. Surface Review and Letters. 2007. 10.1142/S0218625X07009499
[2] Klein and Cardinale. DRM. 1993. 10.1016/0925-9635(93)90250-690250-6)
[3] Singh et al. Phys. Rev. B, Cond. Matt., 2013, 10.1103/PhysRevB.87.235110
[4] Shao et al., J. Appl. Phys., 2012. 10.1063/1.4704698
[5] Migliori et al. J. Appl. Phys, 2008. 10.1063/1.2975190
[6] Hall. Phys. Rev. 1967. 10.1103/PhysRev.161.756
[7] Hakl. Bachelor Thesis of Charles University. 2012. ResearchGate
[8] Band Gap of Silicon. Accessed on Toshiba Website%20has%20a%20band,wide%2Dband%2Dgap%20semiconductor.).
[9] Niquet et al. Phys. Rev. B. 2009 10.1103/PhysRevB.79.245201
[10] Persson and Mirbt. Braz. J. Phys. 10.1590/S0103-97332006000300014.
[11] Barhoumi et al. Solid State Communications. 10.1016/j.ssc.2020.114136
[12] McSkimin and Andreatch. J. Appl. Phys. 10.1063/1.1661636